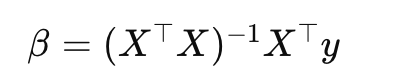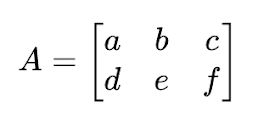- リンクを取得
- ×
- メール
- 他のアプリ
1. 逆行列定義
参照元:https://manabitimes.jp/math/1153
2.何に使われる?
線形回帰
線形回帰では、予測モデルを求めるために最小二乗法を使用することが一般的です。この方法では、正規方程式と呼ばれる方程式を解く必要があり、その解の計算に逆行列が必要になります。
最適化問題
機械学習の多くのアルゴリズムは、ある種の最適化問題を解くことに帰着されます。例えば、勾配降下法などの最適化アルゴリズムでは、逆行列を使用して更新ステップを計算することがあります。
特徴変換
次元削減や特徴抽出のために使用される手法(例えば、主成分分析(PCA))では、共分散行列の逆行列や固有ベクトルを計算する必要があります。
正則化
リッジ回帰やラッソ回帰のような正則化手法では、逆行列が正則化項の計算に使用されます。
3.線形回帰ではどのように逆行列を使用するのか?
線形回帰において逆行列が具体的に使われるケースは、最小二乗法を用いて回帰係数を求める際です。線形回帰モデルは通常、次のような形で表されます。
ここで、yは目的変数のベクトル、Xは説明変数の行列、βは回帰係数のベクトル、εは誤差項です。
最小二乗法では、誤差の二乗和を最小化することで回帰係数βを求めます。具体的には、以下の式を最小化します
この式をβに関して微分し、0に等しいと置くことで、以下の正規方程式を得ます
この方程式をβについて解くために、X⊤Xの逆行列を両辺に左から掛けます
以下が逆行列です。
この逆行列を計算することで、最小二乗法による線形回帰の回帰係数βを求めることができます。
4. 誤差項εを最小化するとは?
誤差項εを最小化するというのは、単純に足した値を少なくするということではありません。通常、誤差項の二乗和(SSE: Sum of Squared Errors)を最小化することを目指します。これは、各データポイントにおける予測値と実際の値との差(誤差)の二乗をすべて足し合わせたものです。
誤差項εiに対して、SSEは次のように表されます
ここで、yiは実際の値、y^iは予測値、nはデータポイントの総数です。
SSEを最小化することで、モデルの予測値が実際の値にできるだけ近くなるように回帰係数を求めることができます。この方法は最小二乗法と呼ばれ、線形回帰モデルで広く使用されています。
誤差の二乗を使用する理由は、正の誤差と負の誤差が相殺されることを防ぎ、より大きな誤差により大きなペナルティを与えるためです。誤差の絶対値を使用する別の方法もありますが、二乗和を使用する方が計算が容易であるため、一般的には二乗和が使用されます。
5. ⊤は何を意味するか?
Tのようなマークは、行列の転置(transpose)を意味します。行列の転置とは、行と列を入れ替えた新しい行列を作る操作のことです。例えば、次の2x3の行列Aがあるとします
この行列Aの転置を取ると、次の3x2の行列A⊤が得られます
行列の転置は、線形代数や機械学習の多くの場面で重要な役割を果たします。
6. 単純な線形回帰モデルの具体的な計算例
説明変数X、目的変数y、回帰係数β、誤差項εが以下のように与えられているとします
ここで、Xの最初の列はすべて1で、バイアス項(切片)に対応しています。Xの二番目の列は説明変数の値です。yは目的変数の値、βは回帰係数、εは誤差項です。
このモデルの予測値y^は、以下のように計算されます
仮に、回帰係数βが次のように推定されたとします
すると、予測値y^は次のようになります
この場合、実際の目的変数yと予測値y^の間には、以下の誤差εが存在します
この計算例では、単純な線形回帰モデルを用いて、説明変数、目的変数、回帰係数、予測値、誤差を計算しています。
実際のデータ分析では、回帰係数βはデータに基づいて推定されるため、予測値と実際の値の間の誤差は異なる可能性があります。
7. 説明変数Xの行列の意味は?
説明変数の行列Xは、データセットの構造に応じて異なるサイズを持ちます。サイズは一般に m×n となります。ここで、m はデータポイント(観測値)の数、n は説明変数(特徴量)の数です。
たとえば、100個のデータポイントがあり、それぞれが3つの説明変数を持つ場合、X は 100×3 の行列になります。一方で、バイアス項(切片)を含める場合、全ての行の最初の列に1を追加し、X は 100×4の行列になります。
8. バイアス項はなぜ必要か?
バイアス項(切片項)は、線形回帰モデルにおいて重要な役割を果たします。バイアス項を含める主な理由は次のとおりです。
モデルの柔軟性の向上
バイアス項を含めることで、線形回帰モデルはデータが原点を通らない場合でも適切にフィットできます。つまり、バイアス項はモデルがデータの平均値をよりよく捉えることを可能にし、モデルの柔軟性を向上させます。
実際のデータに対する適合性の向上
多くの実際のデータセットでは、説明変数がゼロのときに目的変数がゼロになるとは限りません。バイアス項を含めることで、モデルはこのようなケースに対応し、データの実際の傾向をより正確に表現できます。
統計的解釈のため
バイアス項は、説明変数がすべてゼロのときの目的変数の予測値を表します。これは統計的解釈において重要であり、モデルの基準点として機能します。
つまり、1次関数の定数のような役割を果たす。
9. SSEの計算を詳しく
誤差ベクトルε は、実際の目的変数 yと予測値y^の差を要素として持つベクトルです。
SSEは、この誤差ベクトルの各要素を二乗して足し合わせたものです。
ここで、ε⊤ε は、誤差ベクトルの転置と誤差ベクトル自体の積を表し、これにより各要素の二乗和が計算されます。行列の転置が使われるのは、この部分であり、関係ない要素が掛け合わされることはありません。各要素は自身とのみ掛け合わされ、誤差の二乗和が正しく計算されます。
SSEを計算する際には、誤差ベクトル(n×1のベクトル)の転置(1×nのベクトル)と誤差ベクトル自体を掛け合わせます。これにより、n×nの行列ではなく、スカラー値(1×1の行列、つまり数値)が得られます。
具体例を挙げます。
誤差ベクトルが次のような3×1のベクトルであるとします。
このとき、誤差ベクトルの転置は1×3のベクトルになります。
これらを掛け合わせると、次のようになります。
結果は14という数値(スカラー)になります。これが誤差の二乗和(SSE)です。
- リンクを取得
- ×
- メール
- 他のアプリ